2024. 10. 25. 15:35ㆍComputer Engineering/이산수학
1. Ring
1. Ring
- 링은 비어 있지 않은 집합으로, 2가지 이항연산( 덧셈과 곱셈)이 존재하는 구조이다.
- 집합 R이 링이 되기 위한 조건:
- 덧셈: 교환법칙, 결합법칙, 항등원 존재, 역원 존재 → abelian group
- 곱셈: 결합법칙, 분배법칙
- Ring 예시: 정수, 유리수, 실수, 복소수, 정수 행렬은 덧셈과 곱셈이 정의된 Ring의 대표적 예시이다. 예를 들어, 정수에서는 2+3=5이고, 2*3=6이다. 이러한 연산에서 덧셈 항등원은 0이고, 곱셈 항등원은 1이다.
2. Commutative Ring with Unity
- Commutative Ring: 모든 a,b에 대해 ab=ba(곱셈의 교환법칙)이 성립하는 ring
- Ring with Unity: R의 모든 원소에 대해 곱셈 항등원(u)이 존재하여, a*u = u*a = a가 성립하며, u는 0이 아니다.
- Commutative Ring with Unity: 곱셈의 교환법칙 성립하고 항등원이 존재하는 Ring
- 연산 예시: (Z,⊕,⊗)이라는 특별한 연산이 주어진 Ring이 있다.

3. Zero Element (영원)
- Zero Element는 덧셈의 항등원으로, a⊕z=z⊕a=a가 성립하는 원소이다. → additive identity (항등원 개념?)
- 곱셈의 경우, Absorbing Element : z⋅a=a⋅z=z가 성립하는 경우, z가 absorbing element.
- Proper Divisors of Zero(영인수): 두개의 원소가 0이 아닌데도 그 곱셈결과가 0이되는 경우
- 예시: Z6이라는 모듈로 정수 집합에서, 2⋅3=0이지만 2와 3은 둘 다 0이 아니다. 이런 경우를 영 인수라고 한다.
4. Multiplicative Inverse & Unit (곱셈 역원과 유닛)
- 곱셈 Inverse(역원): 가 성립하는 b를 a의 곱셈 역원이라고 한다.
- 예시: 실수 R에서 a=2일 때, 그 역원은 b=1/2이다. 두 수를 곱하면 2⋅1/2=1로 곱셈 항등원이 된다.
- Unit: Ring에서 multiplicative inverse가 존재하는 원소를 Unit이라 부른다. Ring의 모든 원소가 Unit이 되는 경우, 이 Ring을 Field라고 한다.
2. Integral Domain & Field
1. Integral Domain (정역)
- R이 Commutative Ring with Unity인 경우, divisors of zero가 없다면, R을 Integral Domain이라고 부른다.
- 예를 들어, **정수 집합(Z)**에서 2⋅3=6이며, 두 값 모두 0이 아니므로 정수는 Integral Domain이다. 하지만, Z6과 같은 모듈러 집합에서는 2⋅3=0이므로 이 구조는 Integral Domain이 아니다.
2. Field (체)
- Integral Domain 중에서 0이 아닌 원소가 invertible(가역적, 즉 역원이 존재)한 구조를 Field라고 부른다.
- R의 0이 아닌 모든 원소가 Unit이면 Field라고 한다.
- 예를 들어, **유리수(Q)**는 Field. 1/2는 역원인 2와 곱해지면 1이 되는 유닛이므로, 유리수는 Field이다.
- 정수(Z): 정수는 Integral Domain이지만 Field는 아니다.
- 유리수(Q), 실수(R), 복소수(C): 모두 Integral Domain이자 Field이다. 0이 아닌 모든 원소가 invertible하기 때문이다.
3. Integral Domain과 Field의 차이점
- Integral Domain은 곱셈에 대해 zero divisor가 없는 commutative ring이다. 즉 a⋅b=0이 될 때, 반드시 a=0 또는 b=0이어야 한다.
- Field는 Integral Domain이면서, 0이 아닌 모든 원소가 역원을 가진다. 따라서 0이 아닌 임의의 원소 a에 대해 a⋅a^(−1)=1을 만족하는 a^(-1)가 존재해야 한다.

- Ring to Field (Ring에서 Field로 변환): Integral Domain은 곱셈에 대해 zero divisor가 없는 구조이고, Field는 이러한 Integral Domain에서 0이 아닌 모든 원소가 invertible한 경우이다.

3. Ring Properties
1. Ring 기본 성질
- Zero Element와 Additive Inverse(덧셈 역원) unique하다.
- Cancellation of Addition(소거법칙) : 동일한 값이 더해졌을 때 결과가 같다면, 두 더하는 값이 동일해야한다.
- 곱셉에서 Absorbing Element가 성립한다. 즉 a*z=z
- 모든 원소가 곱셈에 대한 inverse를 가지는 것은 아니지만, 만약 inverse가 존재하는 원소라면 그 inverse는 unique하다.
- Ring R이 항등원을 가지고 있다면 그 항등원도 unique하다.
- Integral Domaind에서는 ab=ac일 때 b=c가 성립한다. 즉 곱셈에서 cancellation of multiplication(소거법칙) 성립.
- 만약 F가 Field라면, Integral Domain이다. : zero devisor를 가진다고 가정했을 때 모순 발생
- finite(유한) intgral domain은 field이다.
2. Subring & Ideal
- Subring: Ring R의 부분집합 S로, 덧셈과 곱셈에서 닫혀있고 항등원을 포함하는 구조이다.
- Ideal: Ring R에서 덧셈에 대해 닫혀있고, 곱셈에 대해 흡수성을 가지는 부분집합. 즉 r∈R과 a∈I에 대해 r⋅a∈I가 성립한다. 예를 들어 Z의 부분집합인 6Z는 6의 배수들로 이루어진 ideal이다.
- Kernel: Ring의 homomorphism(동형사상)에서 영원으로 사상되는 원소들의 집합이며, 이 집합은 항상 ideal이 된다.
4. Polynomial Ring
1. Definition of Polynomials
- 주어진 Ring R에서 다항식은 다음과 같은 형태를 따른다.

- R[x]: R위에 정의된 모든 다항식들의 집합을 의미한다.

- Zero Polynomial(영 다항식): 모든 계수가 0인 다항식, 차수는 - ∞ 로 정의.
- Constant Polynomail(상수 다항식): 차수가 0인 다항식이며, 영 다항식도 포함된다.

2. Close Operations of Polynomials(다항식의 닫힘 연산)
- Addition(덧셈): 같은 차수끼리 더한다.
- Multiplication(곱셈): 분배하며 곱을 수행한다.
- 각 항의 계수들에 대해서는 모듈러연산을 수행한 후의 값이 최종 계수가 된다 즉 Z6이라면 6이 0이 된다.
3. Polynomial Ring
- Ring R이 주어졌을 때 , 다항식 연산이 집합 R[x]는 Polynomial Ring이다.
- R이 commutative하면 R[x]도 commutative하다.(교환)
- R이 unity하면 R[x]도 unity하다.(항등원)
- R이 integral domain이면 R[x]도 integral domain이다.
- Degree(차수)에 대한 정리
- R이 integral domain이면

두 다항식의 곱의 차수 = 각 다항식의 차수의 합 - 차수값이 같지 않다면, integral domain이 아니다. 결국 divisor of zero가 있다는 뜻이다.
- R이 integral domain이면
- Roots of Polynomial (다항식의 근)
- Polynomial Divisor or Factor : f(x)*h(x)=g(x) 라 할때, f(x)와 h(x)가 g(x)에 대한 divisor이다.
- Division Algorithm: , deg[r(x)]<deg[f(x)] 를 만족
- Remainger Theorem(나머지 정리): divisor a로 나누어진다고 가정했을 때, 나머지는 f(a)=r(a)=0 또는 c
- Factor Theorem(인수정리): 이면 (x−a)는 f(x)의 인수
- 차수가 n인 다항식은 최대 n개의 근을 가질 수 있다.
5. Finite Field (유한체)
: 유한한 개수의 원소를 가지는 field.
1. Irreducible Polynomail(기약 다항식)
: 나눌 수 없는 다항식
- 차수가 2이상. f(x)를 두 다항식 g(x)와 h(x) (각각 1차 이상)로 인수분해할 수 있다면 약분 가능(reducible) 다항식이라고 한다!
- 만약 인수분해 할 수 없다면 이 f(x)를 기약다항식(irreduciable polynomial) 또는 소수(prime) 다항식이라고 한다.

2. Field F위에서 정의된 다항식 F[x]
- 차수가 1 이하인 0이 아닌 모든 다항식은 기약(약분불가능)이다.
- 차수가 2또는 3인 다항식은 Field F에서 근을 가지는 경우에만 약분 가능하다.
- 만약 다항식의 차수가 3 초과한다면 f(x)=g(x)h(x)일 때, g(x)와 h(x)는 각각 2차 이상일 수 있다. 즉, 차수가 3보다 크면, 인수분해 시 차수 제한 없이 약분될 수 있다!

3. Monic & GCD
- Monic: 다항식의 최고차항 계수가 1인 다항식.
- GCD: 다항식 f(x)와 g(x)의 최대공약수 h(x)는 다음 두 조건을 만족해야 한다.
- h(x)는 f(x)와 g(x)를 나누는 약수이다.
- f(x)와 g(x)의 모든 공약수는 h(x)를 나눈다.
→ 이로 인해 h(x)는 f(x)와 g(x)의 모든 공약수 중에서 가장 차수가 높은 다항식이다.
4. 정수의 최대공약수(GCD)
- 최대공약수 성질: a와 b가 정수일 때, 이 둘의 최대공약수(GCD)를 c라고 정의한다.
- c는 a와 b를 나눌수 있어야한다.
- 정수의 부호는 최대공약수에 영향을 미치지 않는다.
- GCD는 유일하다.(unique)
- a와 b의 모든 공통 약수 d는 c를 나눌 수 있어야 한다.


- GCD는 선형 결합으로 나타낼 수 있다.
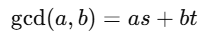
- GCD가 monic이라면 그 GCD는 unique하다.
5. Euclidean Alogorithm
: 두 다항식의 최대공약수를 구할 때 사용, 아무리 큰 숫자라도 GCD 구할 수 있다.
- f(x)와 g(x)의 차수를 비교하여, f(x)의 차수가 더 높으면 g(x)로 나누고 나머지 r(x)를 구한다. 이 과정을 반복(재귀)해 나머지가 0이 될 때까지 진행하며, 마지막에 남은 다항식이 f(x)와 g(x)의 최대공약수gcd가 된다. 나머지가 0이 되었을 때의 다항식이 b(x)라면, gcd(b(x),0)는 monic 다항식으로 표현된다. 이 다항식이 GCD이다.

6.★Relatively Prime (서로소)
: 서로소 다항식은 두 다항식의 GCD가 Field F의 항등원(1)인 경우를 말한다. 즉 f(x)와 g(x)의 GCD가 1이면 두 다항식은 서로소이다.



7. Equivalence Relation (동치 관계)
- 두 다항식 f(x)와 g(x)가 s(x)로 나눈 나머지가 같을 때, 즉 s(x)가 f(x)-g(x)를 나눌 수 있다면 f(x)와 g(x)는 동치이다.
- 이 관계를 통해 모듈러 연산을 나타낼 수 있으며, 이는 다음과 같이 나타낸다.
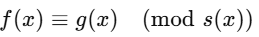
- Equivalence Classes(동치류) : 특정 다항식 s(x)에 대해 f(x)의 나머지 값이 같은 다항식들의 집합 (모듈러)

- 동치류에서의 연산 (operations on equivalence classes)
- 덧셈: [f(x)]+[g(x)]=[f(x)+g(x)]
- 곱셈: [f(x)][g(x)]=[f(x)g(x)]=[r(x)], 여기서 r(x)는 s(x)로 나눈 모듈러 나머지이다.
- F[x] / s(x) : 다항식 s(x)에 대해 모듈러 연산으로 정의된 동치류 집합이다. 즉 F[x] / s(x)는 s(x)로 나눈 나머지에 따라 구분된 모든 동치류의 집합이다.
- F[x] / s(x)는 commutative ring with unity이다. 이는 덧셈과 곱셈 연산에 대해 교환법칙을 만족하며, 항등원이 존재함을 의미한다.
- 만약 s(x)가 F(x)에서 ireeducible하다면, F(x) / s(x)는 Field가 된다.
- 만약 F의 크기가 q이고, s(x)의 차수가 n이면, F[x] / s(x)는 q^n개의 원소를 가진다.
8. characteristic of Ring (특정 원소를 반복해서 더했을 때 0이 되는 최소의 양의 정수)
- Characteristic: Ring R의 특성치는 n*r = 0과 같이 최소의 양의 정수 n으로 정의된다. r은 Ring R의 모든 원소를 포함한다.
- R의 characteristic을 char(R) = n으로 표기한다.
- 만약 이러한 n이 존재하지 않으면, 즉 n*r=0을 만족하는 최소의 n이 없다면, 그 characteristic은 0이라고 정의한다.
- 예를 들어, (정수 모듈러 n)의 경우, 특성치는 n이다.
- 무한 집합인 Z와 Q는 특성치가 0이다.
9. characteristic of Field
- Field F의 characteristic이 0이 아니라면, characteristic은 반드시 소수여야 한다.
- (소수 p에 대한 모듈러 정수 체)는 특성치가 p.
- Z2[x]/(x^2+x+1)은 특성치가 2인 finite field.
- 마찬가지로, Z3[x]/(x^2+x+2)는 특성치가 3.
- Galois Field (갈루아 필드) : finite field는 galois field라고도 불리며, GF(p^t)로 표기된다. 여기서 p는 소수, t는 양의 정수이다.
- 예를 들어, GF(2^3)은 8개의 원소를 가지며, GF(2^8)은 256개의 원소를 가진다.
- 같은 크기의 finite field는 동형(isomorphic)이므로 GF(p^t)는 크기에 따라 유일하다.
- finite field의 characteristic은 디지털 시스템에서 이진법을 사용하는데 매우 유리하다. 특히 AED나 오류수정코드에서 GF(2^n)을 많이 사용한다.
- GF(2^8)에서의 다항식 연산
- 이진 다항식 표현: GF(2^8)의 원소는 이진 문자열로 쉽게 표현할 수 있다. 예를 들어 이진 문자열 01010111은 다항식 x6+x4+x2+x+1을 나타낸다.
- 덧셈 (XOR 연산): 덧셈은 XOR 연산으로 수행된다 - 예: (x6+x4+x2+x+1)+(x7+x4+x3+x+1)=x7+x6+x3+x2
- 곱셈: 다항식 곱셈은 GF(2^8)에서는 단순하지 않으며 특정 기약다항식을 사용해 모듈러 연산을 수행해야 한다. - AES(Advanced Encryption Standard)

- AES와 RS코드에서의 사용
- AES:
- RS(Reed Solomon Code): codeword 길이에 따라 GF(2^8) 또는 GF(2^16) Field에서 코드를 구성하는데, 이는 데이터 보호와 오류 수정에 사용된다.
'Computer Engineering > 이산수학' 카테고리의 다른 글
| Graph Theory (0) | 2024.12.04 |
|---|---|
| Automata 1 (0) | 2024.10.25 |
| 정수론2 (0) | 2024.10.14 |
| 정수론1 (0) | 2024.10.14 |